1. Use logarithm tables correct to 4 significant figures to evaluate. (3 Marks)
√0.07214 X 2.037/69.8
2. Find the equation of the perpendicular bisector of line PQ where the co-ordinates of P and Q are P (-2, 8) and Q (4, 7). (3 Marks)
3. The surface areas of two spheres are 36cm² and 49cm².
If the volume of the smaller sphere is 20.2cm²,
calculate the volume of the larger one. (2 Marks)
4. The marked price of a shirt is Sh. 800. A customer buys the shirt after being given a discount of 13%.
The seller then realizes that he made a profit of 20% on this sale.
Find how much the seller had bought the shirt. (2 Marks)
5. In the grid provided below, show the region R that is satisfied by the three inequalities given below.
Y∂6 – x
y y∊2 (4 Marks)

6. The radius of a cone increases in the ratio 4:3 while it’s height decreases in the ratio 3:4.
Determine the percentage change in the volume of the cone. (3 Marks)
7. Solve for x in the equation (3 Marks )
Log (5x + 75) – 2 Log 3 = Log (2x – 9)
8. Given that a = 3i – 2j + 3k and b = 2i – 4j – 3k where i, j and k are unit vectors,find |2a + 3b| (3 Marks)
9. Make x the subject of the formula in
a=(bx/b+x)⅓
Hence find the value of x when a = 2 and b = 6. (4 Marks)
10. In the figure below, BT is a tangent to the circle at B. AXCT and BXD are straight lines. AX = 6cm, CT = 8cm, BX = 4.8cm and XD = 5cm. (Figure not drawn to scale)
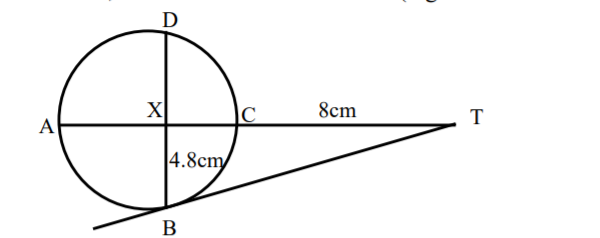
Find the length of
(a) XC (2 Marks)
(b) BT (2 Marks)
11. Simplify 3/√5−2 + 1/√5 leaving your answer in the form a + b√, where a, b and c are rational numbers.(3 Marks)
12. A quantity y varies partly as another quantity x and partly as the square of x. When x = 20, y = 45 and when x = 24, y = 60.
(a) Express y in terms of x (3 Marks)
(b) Find x when y = 75 (1 Mark)
13. Expand (a − x)6 upto the term in(x)3. Use your expansion to estimate the value of (2.99)6to 3 decimal places. (4 Marks)
14. A pipe 3.0m long was cut into three pieces.
The first piece and the second one were measured as 1.3m and 0.94m respectively.
Find the limits within which the length of the third piece lies. (3 Marks)
15. A coffee blender has two brands of coffee, Tamu and Chungu.
A kilogram of Tamu costs Sh. 70 while a kilogram of Chungu costs Shs. 64.
In what ratio should he mix the two brands to make a blend which costs Shs. 68 per kilogram? (2 Marks)
16. Find the centre and radius of a circle whose equation is x2+ y2+ 8x + y2 – 2y – 1 = 0 (3 Marks)
SECTION II (50 Marks): Answer ANY FIVE questions in this section in the spaces provided.
17. In a Science class ⅔ of the class are boys and the rest are girls. 80% of the boys and 90% of the girls are right handed.
The probability that the right handed student will break a test tube in any session is ⅒ and that for the left handed student is 3/10 ,regardless of whether boy or girl.
(a) Draw a tree diagram to represent this information. (2 Marks)
(b) Using the tree diagram drawn, find the probability that:
(i) A student chosen at random from the class is left handed (2 Marks)
(ii) A test tube is broken by a left handed student. (2 Marks)
(iii) A test tube is broken by a right handed student. (2 Marks)
(iv) A test tube is not broken in any session (3 Marks)
18. Matrix P is given by (4 7 5 8 )
(a) Find P-1 (2 Marks)
(b) Two institutions, Katulani High School and Nthia High School purchased beans at Sh. b per bag and maize at Sh. m per bag.
Katulani purchased 8 bags of beans and 14 bags of maize for KSh. 47,600. Nthia purchased 10 bags of beans and 16 bags of maize for KSh. 57,400.
(i) Form a matrix equation to represent the information above. (2 Marks)
(ii) Use matrix P-1 to find the prices of one bag of each item. (3 Marks)
(c) The price of beans later went up by 5% and that of maize remained constant.
Katulani bought the same quality of beans but spent the same total of money as before on the two items.
State the new ratio of beans to maize. (3 Marks)
19. James’ earning are as follows:-
Basic salary Sh. 38,000 p.m
House allowance Sh. 14,000 p.m
Travelling allowance Sh. 8,500 p.m
Medical allowance Sh. 3,300
The table for the taxable income is as shown below.
Income tax in K£ p.a | Tax in Sh. per pound |
|---|---|
| 1 600 | 2 |
| 6001 12000 | 3 |
| 12001 18000 | 4 |
| 1001 24000 | 5 |
| 24001 30000 | 6 |
| 30001 36000 | 7 |
| 36001 42000 | 8 |
| 42001 48000 | 9 |
| Over 48000 | 10 |
(a) Calculate James’ taxable income in K£ p.a. (2 Marks)
(b) Calculate James’s P.A.YE if he is entitled to a tax relief of Sh. 18000 p.a. (4 Marks)
(c) James is also deducted the following per month:- NHIF Sh. 320 Pension scheme Sh. 1000 Co-operative shares Sh. 2000 Loan repayment Sh. 5000 Interest on loan Sh. 500
(i) Calculate James’ total deduction per month in KSh. (2 Marks)
(ii) Calculate his net salary per month (2 Marks)
20. Three consecutive terms of a geometric progression are 32+1, 9x and 81 respectively.
(a) Calculate the value of x (3 Marks)
(b) Find the common ratio of the series. (1 Mark)
(c) Calculate the sum of the first 4 terms of this series. (3 Marks)
(d) Given that the fifth and the seventh terms of the G.P form the first two consecutive terms of an arithmetic sequence,
calculate the sum of the first 20 terms of the sequence. (3 Marks)
21. A tank has two inlet taps P and Q and an outlet tap R. When empty, the tank can be filled by tap P alone in 4½hour or by tap Q alone in 3 hours.
When full, the tap can be emptied in 2 hours by tap R.
2 (a) The tank is initially empty. Find how long it would take to fill up the tank
(i) If tap R is closed and taps P and Q are opened at the same time. (2 Marks)
(ii) If all the three taps are opened at the same time. (2 Marks)
(b) The tank is initially empty and the three taps are opened as follows:-
P at 8.00 a.m
Q at 8.45 a.m
R at 9.00 a.m
(i) Find the fraction of the tank that would be filled by 9.00 a.m (3 Marks)
(ii) Find the time the tank would be fully filled up (3 Marks)
22. In the figure below M and N are points on OQ and QP such that OM:MQ = 2:3 and QN : NP = 2:1. ON and PM intersect at X.
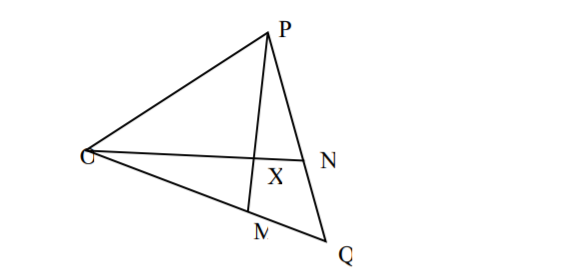
(a) Given that OP = p and OQ = q. Express in terms of p and q
(i) ON (2 Marks)
(ii) PM (2 Marks)
(b) Given that OX = hON and PX = kPM where h and k are scalars,
(i) Determine the values of h and k. (5 Marks)
(ii) Determine ratio in which X divides PM. (1 Mark)
23. The figure below shows a circle centre O, PQRS is a cyclic quadrilateral and QOS is a straight line.
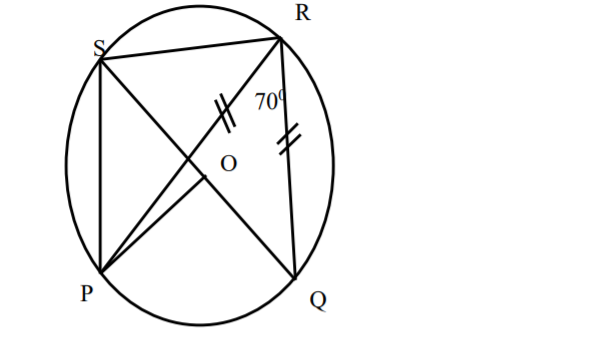
Giving reasons for your answers, find the size of
(a) Angle PRS (2 Marks)
(b) Angle POQ (2 Marks)
(c) Angle QSR (3 Marks)
(d) Reflex angle POS (3 Marks)
24. (a) Complete the table below for y = x³ + 4×2 – 5x – 5 (2 Marks)
x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|
y = x³+ 4x² – 5x – 5 | | | 19 | | | -5 | |
(b) On the grid provided, draw the graph of y = x3 + 4×2 – 5x – 5 for -5 ∂ x ∂ 2 (3 Marks)

(c) (i) Use the graph to solve the equation x³ + 4×2 – 5x – 5 = 0 (2 Marks)
(ii) By drawing a suitable straight line on the graph, solve the equation (3 Marks) x3 + 4×2 – 5x – 5 = -4x – 1
Kenya High Mock Mathematics Paper 2 2021 – With Marking Scheme
1. Use logarithm tables correct to 4 significant figures to evaluate. (3 Marks)
√0.07214 X 2.037/69.8
1. No. Log
0.7214 2.8582
20.37 0.3090
1.1672 x 1/3
69.8 1.7224
1.8439
3.8785
7.560 x 10-3
2. Find the equation of the perpendicular bisector of line PQ where the co-ordinates of P and Q are P (-2, 8) and Q (4, 7). (3 Marks)
Co-ordinates of mid-point M:
OM = 1/2(OP + OQ)
Hence M (1,7.5)
Gradient of PQ = ( 7−8/4−−2 ) = −1/6
Equation of bisector of PQ at
−7.5/−1 = 6
y – 7.5 = 6x -6
y = 6x + 3/2
= 1/2 [(−2 8 + (4 7 ))] = 1/2 (2 15 ) = (1 7.5 )
3. The surface areas of two spheres are 36cm² and 49cm².
If the volume of the smaller sphere is 20.2cm²,
calculate the volume of the larger one. (2 Marks)
A.S.F = 36/49, L.S.F = 6/9 = 2/3
V.S.F = 2³/3³ = 8/27
8/27 = 20.2/ , v = 68.175cm³
4. The marked price of a shirt is Sh. 800. A customer buys the shirt after being given a discount of 13%.
The seller then realizes that he made a profit of 20% on this sale.
Find how much the seller had bought the shirt. (2 Marks)
87/100 x 800 = 696 (selling point)
B.P x 120/100 = 696, B.P = KSh. 580
5. In the grid provided below, show the region R that is satisfied by the three inequalities given below.
Y∂6 – x
y y∊2 (4 Marks)

6. The radius of a cone increases in the ratio 4:3 while it’s height decreases in the ratio 3:4.
Determine the percentage change in the volume of the cone. (3 Marks)

7. Solve for x in the equation (3 Marks )
Log (5x + 75) – 2 Log 3 = Log (2x – 9)
Log (5x + 75) – Log (2x – 9) = Log3²
Log(5+75) = Log3²
2+9
5+75 = 9
2+9
5x + 75 = 9(2x – 9)
156 = 13x
x = 12
8. Given that a = 3i – 2j + 3k and b = 2i – 4j – 3k where i, j and k are unit vectors,find |2a + 3b| (3 Marks)
2a = 2(3i – 2j + 3k
= 6i – 4j + 6k
3b = 3(2i – 4j – 3k)
= 6i – 12i – 9k
2a – 3b = 8j + 15k
|2a – 3b) = √64 + 225
= 17
9. Make x the subject of the formula in
a=(bx/b+x)⅓
Hence find the value of x when a = 2 and b = 6. (4 Marks)
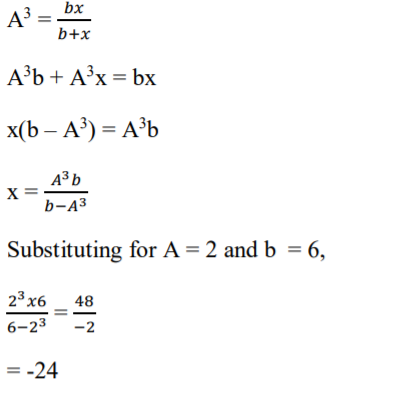
10. In the figure below, BT is a tangent to the circle at B. AXCT and BXD are straight lines. AX = 6cm, CT = 8cm, BX = 4.8cm and XD = 5cm. (Figure not drawn to scale)

Find the length of
(a) XC (2 Marks)
) 6(XC) = 5 x 4.8
XC = 5 4.8/6 = 4cm
(b) BT (2 Marks)
8 x (8 + 4 + 6) = BT2
BT = √144 = 12cm
11. Simplify 3/√5−2 + 1/√5 leaving your answer in the form a + b√, where a, b and c are rational numbers.(3 Marks)
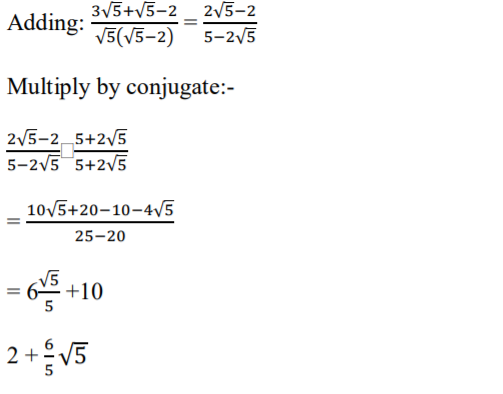
12. A quantity y varies partly as another quantity x and partly as the square of x. When x = 20, y = 45 and when x = 24, y = 60.
(a) Express y in terms of x (3 Marks)
(b) Find x when y = 75 (1 Mark)
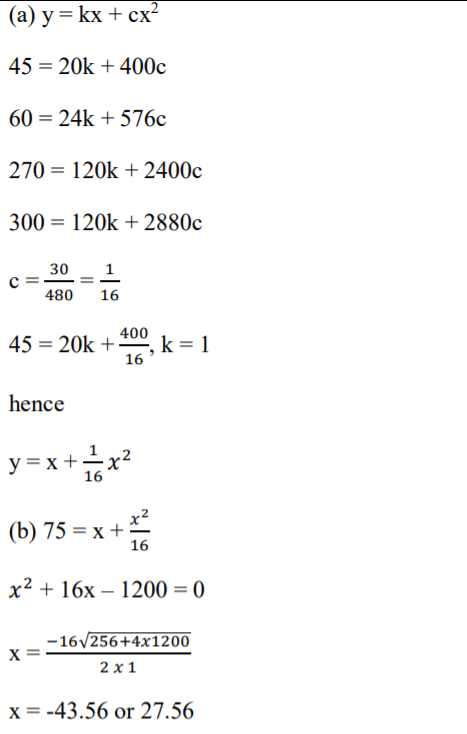
13. Expand (a − x)6 upto the term in(x)3. Use your expansion to estimate the value of (2.99)6to 3 decimal places. (4 Marks)
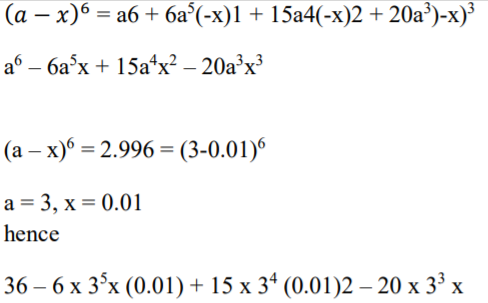
(0.01)³
729 – 14.58 + 0.1215 – 0.00054
= 714.54096
= 714.541
14. A pipe 3.0m long was cut into three pieces.
The first piece and the second one were measured as 1.3m and 0.94m respectively.
Find the limits within which the length of the third piece lies. (3 Marks)
14. Third piece
Max length: 3.05 – (1.25 + 0.935)
= 0.865m
Min length: 2.95 (1.35 + 0.945)
= 0.655m
Hence 0.655 to 0.865m
15. A coffee blender has two brands of coffee, Tamu and Chungu.
A kilogram of Tamu costs Sh. 70 while a kilogram of Chungu costs Shs. 64.
In what ratio should he mix the two brands to make a blend which costs Shs. 68 per kilogram? (2 Marks)
1kg of Tamu mixed with x kg of Chungu (70 x 1) + (64 x x) = 68 x (1 + x)
70 + 64x = 68 + 68x
x = ½
Tamu: Chungu = 1: x = 1:½
= 2:1
16. Find the centre and radius of a circle whose equation is x2+ y2+ 8x + y2 – 2y – 1 = 0 (3 Marks)
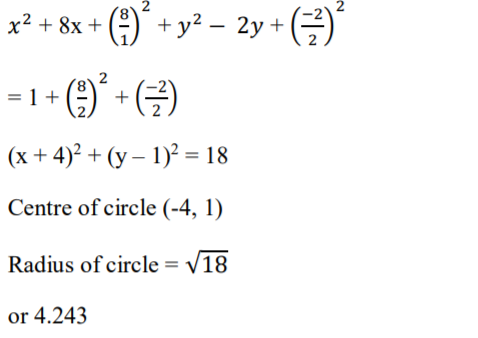
SECTION II (50 Marks): Answer ANY FIVE questions in this section in the spaces provided.
17. In a Science class ⅔ of the class are boys and the rest are girls. 80% of the boys and 90% of the girls are right handed.
The probability that the right handed student will break a test tube in any session is ⅒ and that for the left handed student is 3/10 ,regardless of whether boy or girl.
(a) Draw a tree diagram to represent this information. (2 Marks)
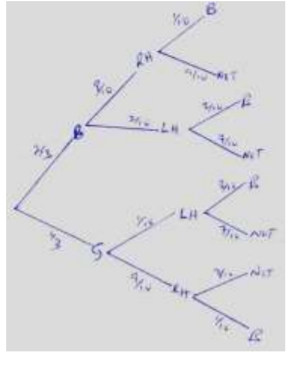
(b) Using the tree diagram drawn, find the probability that:
(i) A student chosen at random from the class is left handed (2 Marks)
(b) (i) 2/3×2/10+1/3×1/10
= 4/30 + 1/30 = 5/30 = 1/6
(ii) A test tube is broken by a left handed student. (2 Marks)
(iii) A test tube is broken by a right handed student. (2 Marks)
(iv) A test tube is not broken in any session (3 Marks)
2/3 x 2/10 x 3/10 + 1/3 x 3/10
= 12/300 + 3/300
= 15/300
= 1/20
18. Matrix P is given by (4 7 5 8 )
(a) Find P-1 (2 Marks)
(b) Two institutions, Katulani High School and Nthia High School purchased beans at Sh. b per bag and maize at Sh. m per bag.
Katulani purchased 8 bags of beans and 14 bags of maize for KSh. 47,600. Nthia purchased 10 bags of beans and 16 bags of maize for KSh. 57,400.
(i) Form a matrix equation to represent the information above. (2 Marks)
(ii) Use matrix P-1 to find the prices of one bag of each item. (3 Marks)

− 4/3 28700 )
(b m) = (3500 1400 )
Bag of beans cost Sh. 3500
Bag of maize cost Sh. 1400
(c) The price of beans later went up by 5% and that of maize remained constant.
Katulani bought the same quality of beans but spent the same total of money as before on the two items.
State the new ratio of beans to maize. (3 Marks)
115/100 x 3500 = 4025
8 x 4025 = 32400
47600 – 32400 = 15400
=1400m = 15400
m = 11 bags
=Ratio 8:11
19. James’ earning are as follows:-
Basic salary Sh. 38,000 p.m
House allowance Sh. 14,000 p.m
Travelling allowance Sh. 8,500 p.m
Medical allowance Sh. 3,300
The table for the taxable income is as shown below.
Income tax in K£ p.a | Tax in Sh. per pound |
|---|---|
| 1 600 | 2 |
| 6001 12000 | 3 |
| 12001 18000 | 4 |
| 1001 24000 | 5 |
| 24001 30000 | 6 |
| 30001 36000 | 7 |
| 36001 42000 | 8 |
| 42001 48000 | 9 |
| Over 48000 | 10 |
(a) Calculate James’ taxable income in K£ p.a. (2 Marks)
(b) Calculate James’s P.A.YE if he is entitled to a tax relief of Sh. 18000 p.a. (4 Marks)
(c) James is also deducted the following per month:- NHIF Sh. 320 Pension scheme Sh. 1000 Co-operative shares Sh. 2000 Loan repayment Sh. 5000 Interest on loan Sh. 500
(i) Calculate James’ total deduction per month in KSh. (2 Marks)
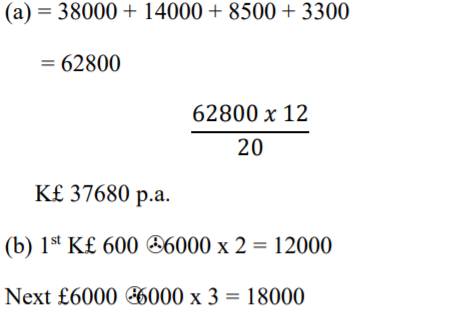

(ii) Calculate his net salary per month (2 Marks)
Net salary = 62800 – 23900
=38,900
20. Three consecutive terms of a geometric progression are 32+1, 9x and 81 respectively.
(a) Calculate the value of x (3 Marks)
(b) Find the common ratio of the series. (1 Mark)
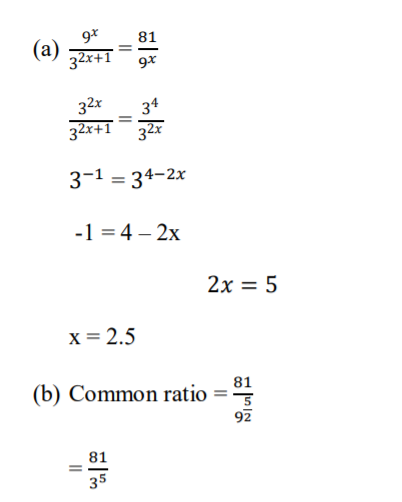
(c) Calculate the sum of the first 4 terms of this series. (3 Marks)
(d) Given that the fifth and the seventh terms of the G.P form the first two consecutive terms of an arithmetic sequence,
calculate the sum of the first 20 terms of the sequence. (3 Marks)
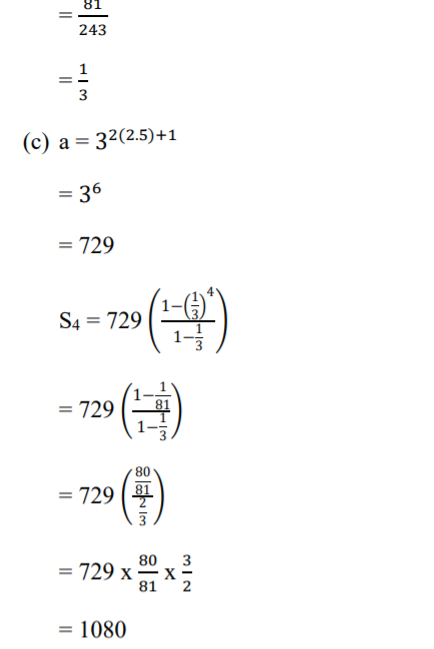
21. A tank has two inlet taps P and Q and an outlet tap R. When empty, the tank can be filled by tap P alone in 4½hour or by tap Q alone in 3 hours.
When full, the tap can be emptied in 2 hours by tap R.
2 (a) The tank is initially empty. Find how long it would take to fill up the tank
(i) If tap R is closed and taps P and Q are opened at the same time. (2 Marks)
(ii) If all the three taps are opened at the same time. (2 Marks)
(b) The tank is initially empty and the three taps are opened as follows:-
P at 8.00 a.m
Q at 8.45 a.m
R at 9.00 a.m
(i) Find the fraction of the tank that would be filled by 9.00 a.m (3 Marks)
(ii) Find the time the tank would be fully filled up (3 Marks)

= 12½ hrs
Time taken for taken to fill up
= 0900
1230
2130 hrs
or 9.30 p.m
22. In the figure below M and N are points on OQ and QP such that OM:MQ = 2:3 and QN : NP = 2:1. ON and PM intersect at X.

(a) Given that OP = p and OQ = q. Express in terms of p and q
(i) ON (2 Marks)
(ii) PM (2 Marks)
(b) Given that OX = hON and PX = kPM where h and k are scalars,
(i) Determine the values of h and k. (5 Marks)
(ii) Determine ratio in which X divides PM. (1 Mark)
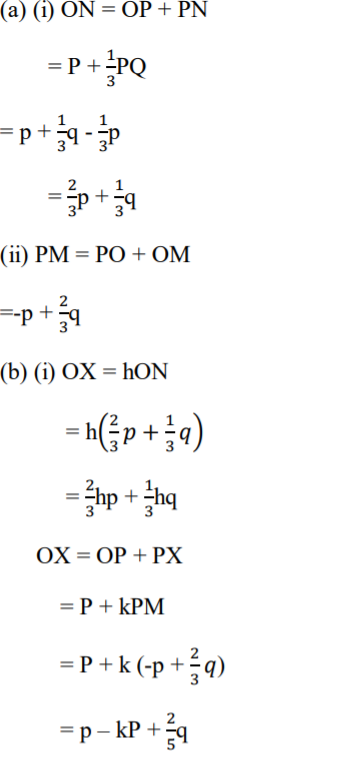

23. The figure below shows a circle centre O, PQRS is a cyclic quadrilateral and QOS is a straight line.

Giving reasons for your answers, find the size of
(a) Angle PRS (2 Marks)
QRS = 900 (Subst. by the remainder)
PRS = 90 – 70 = 200
(b) Angle POQ (2 Marks)
POQ = 2 x 700 = 1400
at centre is twice at circumference
(c) Angle QSR (3 Marks)
∠RQP = 180−70/2 = 55°( Base angles of a ⊗)
RQP and PSE are supplementary (cyclic quadrilateral)
4 PSR = 180 – 55 = 1250
QSR = 125 – 70
= 55°
(d) Reflex angle POS (3 Marks)
∠PSQ = ∠PRQ = 70° (Subst. by same arc)
QSP = SPO = 70° (base angles of isosceles ⊗
Reflex POS = 360 – 40
= 320°
24. (a) Complete the table below for y = x³ + 4×2 – 5x – 5 (2 Marks)
x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|---|---|---|
| y | -5 | 15 | 19 | 13 | 3 | -5 | -5 | 9 |
(b) On the grid provided, draw the graph of y = x3 + 4×2 – 5x – 5 for -5 ∂ x ∂ 2 (3 Marks)
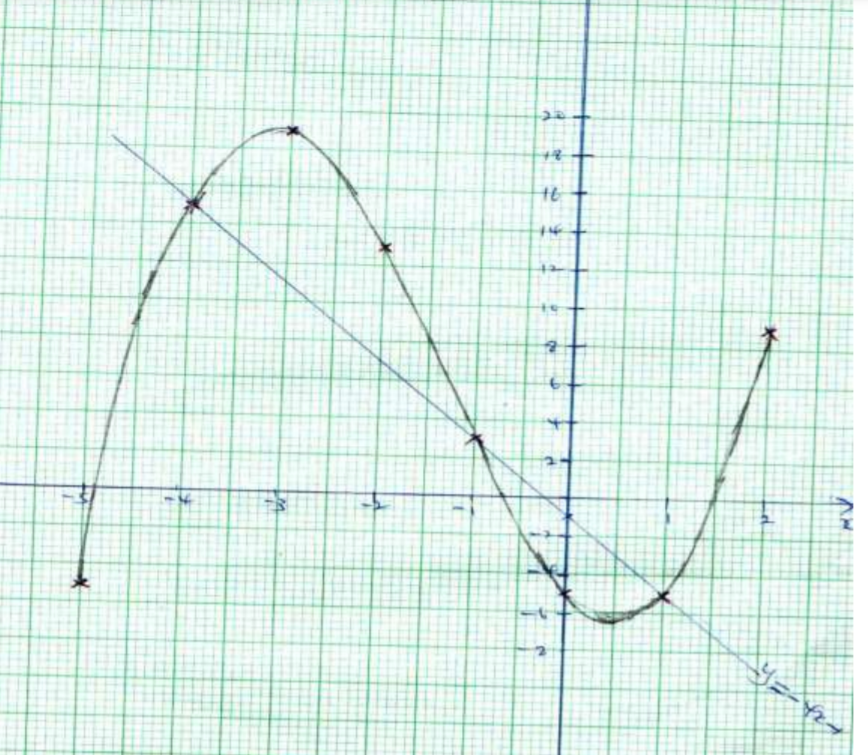
(c) (i) Use the graph to solve the equation x³ + 4×2 – 5x – 5 = 0 (2 Marks)
x = -4.85
x = -0.7
x = 1.5
(ii) By drawing a suitable straight line on the graph, solve the equation (3 Marks) x3 + 4×2 – 5x – 5 = -4x – 1
x³ + 4x² – 5x – 5 = -4x – 1 x³ + 4x² – x – 4 = 0
y = x³ – 4x² – 5x = 5 0 = x³ – 4x² – x – 4
y = -4x – 1
x 0 1
y -1 -5
x = -4
x = 1

