1. Evaluate-12 -(3x)4-(-20)/– 6 x 6 +(-6) (2 Marks)
2. Mr. Owino spends 1/4 of his salary on school fees. He spends 2/3 of the remainder on food and a fifth of what is left on transport.
He saves the balance. In certain month he saved Sh. 3400. What was his salary? (3 marks)
3. Simplify: (3 Marks)
2y²-3xy-2x²/4y²-x²
4. Find x if32x+3+ 1 = 28 (2 Marks)
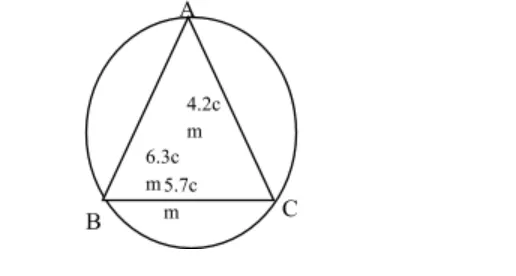
5. The circle below whose area is 18.05cm² circumscribes triangle ABC where AB = 6.3cm, BC = 5.7cm and AC = 4.2cm.
Find the area of the shaded part. (4 Marks)
6. A salesman gets a commission of 2.4% on sales up to Sh. 100,000. He gets additional commission of 1.5% on sales above this.
Calculate the commission he gets for sales worth Sh. 280,000. (3 Marks)
7. A rectangle whose area is 96m² is such that its length is 4metres longer than its width. Find.
(a) Its dimensions (2 Marks)
(b) Its perimeter (1 Mark)
8. Give sin (90 – a) = 1/2 find without using trigonometric tables the value of cos a . (2 Marks)
9. In triangle ABC below, AC = BC, AB is parallel to DE, AB = 15cm, DE = 7.5cm and BE = 6cm.
(a) Calculate Length CE (2 Marks)
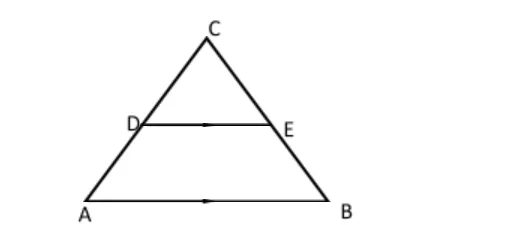
(b) Area of quadrilateral ABED. (2 Marks)
10. A measuring cylinder of base radius 5cm contains water whose level reads 6cm high.
A spherical object is immersed in the water and the new level reads 10cm.
Calculate the radius of the spherical object (3 Marks)
11. Using a ruler and pair of compasses only, construct triangle ABC in which AB = 6cm, BC = 8cm and angle ABC = 450. Drop a perpendicular from A to BC to meet line BC at M.
(i) Measure AM and AC. (4 Marks)
12. In a book store, books packed in cartons are arranged in rows such that there are 50 cartons in the first row, 48 cartons in the next row, 46 in the next and so on. How many cartons will there be in the 8th row? (2 Marks)
(a) If there are 20 rows in total, find the total number of cartons in the book store. (2 Marks)
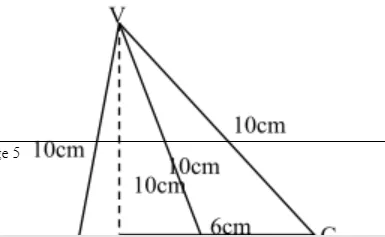
13. Draw the net of the solid below and calculate the total surface area of its faces. (3 Marks)
14. Town X is 20km in a bearing of 0600 from Y, and Z is 30km in the direction 1500 from Y. Using the scale 1cm represents 5km, find by scale drawing:
(a) The bearing of Y from Z. (2 Marks)
(b) The distance of X from Z. (2 Marks )
15. Solve for x in 22x – 18 x 2x = 40 (3 Marks)
16. Oketch sells his car to Jane and makes a profit of 20%.
Jane sells the same to Issa at Sh.180, 000, making a loss of 10%.
Determine the price at which Oketch bought the car. (3 Marks)
Section II (50 Marks):
Answer ANY five questions in this section in the spaces provided.
17. The distance between towns A and B is 360km. A minibus left town A at 8.15 a.m. and traveled towards town B at an average speed of 90km/hr.
A matatu left town B two and a third hours later on the same day and travelled towards A at average speed of 110km/hr.
(i) At what time did the two vehicles meet? (4 Marks)
(ii) How far from A did the two vehicles meet? (2 Marks)
(b) A motorist started from his home at 10.30 a.m. on the same day as the matatu and travelled at an average speed of 100km/h.
He arrive at B at the same time as the minibus.
Calculate the distance from A to his house. (4 Marks)
18. Karis owns a farm that is triangular in shape as shown below.
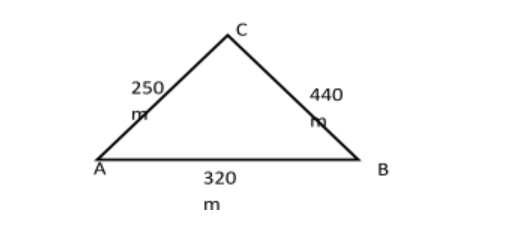
(a) Calculate the size of angle BAC (2 Marks)
(b) Find the area of the farm in hectares (3 Marks)
18. Karis wishes to irrigate his farm using a sprinkler machine situated in the farm such that it is equidistant from points A, B and C.
(i) Calculate the distance of the sprinkler from point C. (2 Marks)
(ii) The sprinkler rotates in a circular motion so that the maximum point reached by the water jets is the vertices A, B and C.
Calculate the area outside his farm that will be irrigated. (3 Marks)
19. A ship leaves port M and sails on a bearing of 0500 heading towards island L. Two Navy destroyers sail from a naval base N to intercept the ship.
Destroyer A sails such that it covers the shortest distance possible.
Destroyer B sails on a bearing of 200 to L. The bearing of N from M is 1000 and distance NM = 300KM. Using a scale of 1cm to represent 50km, determine:-
(i) the positions of M, N and L. (3 Marks)
(ii) the distance travelled by destroyer A (3 Marks)
(iii) the distance travelled by destroyer B. (2 Marks)
(iv) the bearing of N from L. (2 Marks)
20. A number of people agreed to contribute equally to buy books worth KSh. 1200 for a school library.
Five people pulled out and so the others agreed to contribute an extra Shs. 10 each.
Their contributions enabled them to buy books worth Shs. 200 more than they originally expected.
(a) If the original numbers of people was x, write an expression of how much each was originally to contribute. (1 Mark)
(b) Write down two expressions of how much each contributed after the five people pulled out. (2 Marks)
(c) Calculate the number of people who made the contribution. (5 Marks)
(d) Calculate how much each contributed. (2 Marks)
21. Using a ruler and a pair of compasses only, draw a parallelogram ABCD, such that angle DAB = 750. Length AB = 6.0cm and BC = 4.0cm.
From point D, drop a perpendicular to meet line AB at N. (7 Marks)
(i) Measure length DN (1 Mark)
(ii) Find the area of the parallelogram. (2 Marks)
22. The following measurements were recorded in a field book of a farm in metres (xy = 400m)
| Y | ||
|---|---|---|
| 400 | ||
| C60 | 350 | |
| 300 | 120D | |
| 240 | 100E | |
| 220 | 160F | |
| B100 | 140 | |
| A120 | 80 | |
| X |
(a) Using a scale of 1cm representing 4000cm, draw an accurate map of the farm. (3 Marks)
(b) If the farm is on sale at Kshs. 80,000.00 per hectare, find how much it costs. (7 Marks)
23. The table shows marks obtained by 100 candidates at Goseta Secondary School in Biology examination.
| Marks | 15-24 | 25-34 | 35-44 | 45-54 | 55-64 | 65-74 | 75-84 | 85-94 |
|---|---|---|---|---|---|---|---|---|
| Frequency | 6 | 14 | 24 | 14 | x | 10 | 6 | 4 |
(a)Determine the value of x (2 Marks)
(b) State the modal class (1 Mark)
(c) Calculate the median mark (2 Marks)
(d) Calculate the mean mark (5 Marks)
24. In the diagram below, two circles, centres A and C and radii 7cm and 24cm respectively intersect at B and D. AC = 25cm.
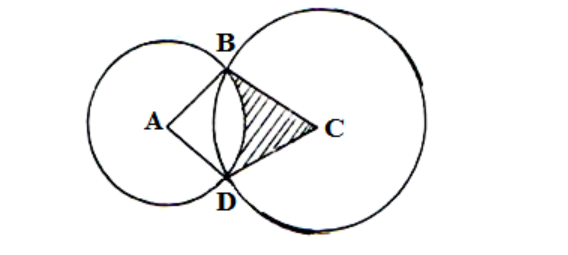
(a) Show that angle ABC = 900. (3 Marks)
(b) Calculate
(i) the size of obtuse angle BAD (3 Marks)
(ii) the area of the shaded part (4 Marks)
Marking Scheme
1. Evaluate-12 -(3x)4-(-20)/– 6 x 6 +(-6) (2 Marks)
16+20/-12-6
36/-18
= -2
2. Mr. Owino spends 1/4 of his salary on school fees. He spends 2/3 of the remainder on food and a fifth of what is left on transport.
He saves the balance. In certain month he saved Sh. 3400. What was his salary? (3 marks)
Food = 12
Trans = 120
Rem = 14
Fraction of saving
= 1 – (1/2+ 1/20 + 1/4) = 1 – 16/20 = 4/20
Salary = 3400 x 20/4
= KSh. 17000
3. Simplify: (3 Marks)
2y²-3xy-2x²/4y²-x²
y-2x(2y+x)/2y-x(2y+x)
y-2x/2y-x
4. Find x if32x+3+ 1 = 28 (2 Marks)
32x+3+ 1 = 28
32x+3 = 27
32x x 33 = 33
27 x 32x = 27
32x = 10
2x = 0
x = 0
5. The circle below whose area is 18.05cm² circumscribes triangle ABC where AB = 6.3cm, BC = 5.7cm and AC = 4.2cm.
Find the area of the shaded part. (4 Marks)
S = 5.7+4.2+6.32 = 8.1
= √8.18.1-5.78.1-4.28.1-6.3
= √8.1 x 2.4 x 3.9 x 1.8 = 11.68
Shaded area = 18.05 – 11.68
= 6.368cm²

6.A salesman gets a commission of 2.4% on sales up to Sh. 100,000. He gets additional commission of 1.5% on sales above this.
Calculate the commission he gets for sales worth Sh. 280,000. (3 Marks)
2.4/100 x 100,000 = 2400
3.9/100 x 180,000 = 7020
= 9420
7. A rectangle whose area is 96m² is such that its length is 4metres longer than its width. Find.
(a) Its dimensions (2 Marks)
x² + 4x – 96 = 0
(x-8) (x + 12) = 0
x = 8
Length = 12
Width = 8
(b) Its perimeter (1 Mark)
2 (8 + 12) = 40m
8. Give sin (90 – a) = 1/2 find without using trigonometric tables the value of cos a . (2 Marks)
Sin-1 0.5 = (90 – a)
600 = 900 – a
a = 300
Cos 300
Cos a = √3/2
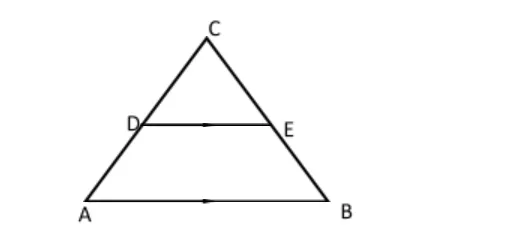
9. In triangle ABC below, AC = BC, AB is parallel to DE, AB = 15cm, DE = 7.5cm and BE = 6cm.
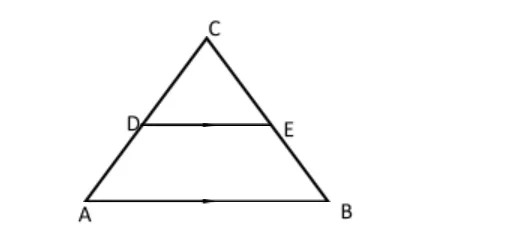
(a) Calculate Length CE (2 Marks)
CE/BC = DE/AB
x/x+6 = 7.5/15
x = 6
(b) Area of quadrilateral ABED. (2 Marks)
√6²-3.75²- = 4.684
AB = 2 x 4.684 = 9.368
A = 1/2 x 15 x 9.368 – 1/2 x 7.5 x 4.684
= 52.698
10. A measuring cylinder of base radius 5cm contains water whose level reads 6cm high.
A spherical object is immersed in the water and the new level reads 10cm.
Calculate the radius of the spherical object (3 Marks)
22/7 x 5² (10 – 6) = 314.29cm³ 4/3 x 22/7r³ = 314.29
r = 4.217
11. Using a ruler and pair of compasses only, construct triangle ABC in which AB = 6cm, BC = 8cm and angle ABC = 450. Drop a perpendicular from A to BC to meet line BC at M.
(i) Measure AM and AC. (4 Marks)
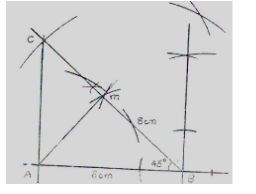
12. In a book store, books packed in cartons are arranged in rows such that there are 50 cartons in the first row, 48 cartons in the next row, 46 in the next and so on. How many cartons will there be in the 8th row? (2 Marks)
(a) If there are 20 rows in total, find the total number of cartons in the book store. (2 Marks)
50,48,46,……………
T8 = 50 + 7x (-2)
= 36
S2 = 20/2 (2 x 50 + (20 – 1) (x – 2)
= 620
13. Draw the net of the solid below and calculate the total surface area of its faces. (3 Marks)
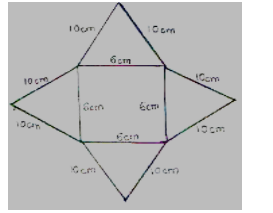
Surface area of base = 6cm x 6cm = 36cm²
Area of sides (flaps) = ( ½ x 6cm x 8cm)4 = 96cm²
Total surface area = 36cm² + 96cm² = 132cm²
14. Town X is 20km in a bearing of 0600 from Y, and Z is 30km in the direction 1500 from Y. Using the scale 1cm represents 5km, find by scale drawing:
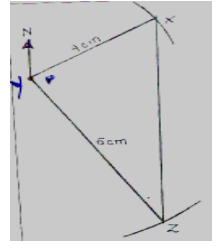
(a) The bearing of Y from Z. (2 Marks)
324°
(b) The distance of X from Z. (2 Marks )
(7.2 x 5) km = 36km
15. Solve for x in 22x – 18 x 2x = 40 (3 Marks)
22x – 18 x 2x – 40 = 0
2×2 – 18 x 2x-40 = 0
Let 2x be t
t2 – 18t – 40 = 0
t(t – 20) + 2(t – 20) = 0
(t + 2)(t-20) = 0
Either
t – 20 = 0 t = 20
or t + 2 = 0 t = -2
but t = 2x
for 2x = -2 there are no real values
but for 2x = 20
xlog2/log = log 20/log 2
x = 4.32 (2 dps)
16. Oketch sells his car to Jane and makes a profit of 20%.
Jane sells the same to Issa at Sh.180, 000, making a loss of 10%.
Determine the price at which Oketch bought the car. (3 Marks)
90/100x = 180,000
x = 180000/90 x 100
= 200000
120/100y = 200000
BP ⇒200000/120 x 100 = 166,666.66
Section II (50 Marks):
Answer ANY five questions in this section in the spaces provided.
17. The distance between towns A and B is 360km. A minibus left town A at 8.15 a.m. and traveled towards town B at an average speed of 90km/hr.
A matatu left town B two and a third hours later on the same day and travelled towards A at average speed of 110km/hr.
(i) At what time did the two vehicles meet? (4 Marks)
= 73 x 90 = 210km
Remaining distance = 360 – 210 = 150km
As = 90 + 110 = 200km
Time for meeting = 150km200km/hr = 0.75 hrs
= 45 mins
Meeting time = 10.35 + .45 = 11.20 a.m
(ii) How far from A did the two vehicles meet? (2 Marks)
Distance from A 210 + (0.75 x 90)
= 210 + 67.5
= 277.5 km
(b) A motorist started from his home at 10.30 a.m. on the same day as the matatu and travelled at an average speed of 100km/h.
He arrive at B at the same time as the minibus.
Calculate the distance from A to his house. (4 Marks)
Time minibus arrived at B
Time = D/S = 360/90 = 4 hrs
= 8.15 + 4 hrs = 12.15 p.m
Time taken by the tourist to arrive
B = 12.15 pm – 10.30 a.m = 1 hr 45 min
= 14560 x 100
= 175km
∴ Home to B = 175km
Home to A = 360 – 175
= 185km
18. Karis owns a farm that is triangular in shape as shown below.

(a) Calculate the size of angle BAC (2 Marks)
Cosθ = 250²+320²-4402² / 2✘250✘ 320
θ = 100.33°
A = 1/2x 250 x 320 Sin 100.33
39351/6510000
= 3.9352 ha
(b) Find the area of the farm in hectares (3 Marks)
2R = 440/Sin 100.33
R = 223.6
A = 22/7 x 223.6² – 39351.65
= 117,781.7m²
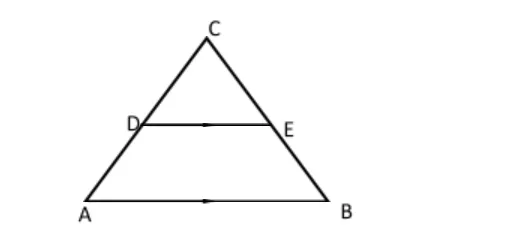
(ii) The sprinkler rotates in a circular motion so that the maximum point reached by the water jets is the vertices A, B and C.
Calculate the area outside his farm that will be irrigated. (3 Marks)
19. A ship leaves port M and sails on a bearing of 0500 heading towards island L. Two Navy destroyers sail from a naval base N to intercept the ship.
Destroyer A sails such that it covers the shortest distance possible.
Destroyer B sails on a bearing of 200 to L. The bearing of N from M is 1000 and distance NM = 300KM. Using a scale of 1cm to represent 50km, determine:-
(i) the positions of M, N and L. (3 Marks)
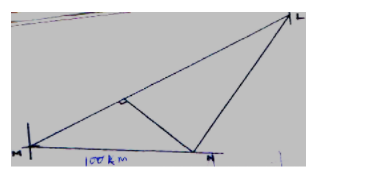
(ii) the distance travelled by destroyer A (3 Marks)
4.4 x 50 = 220km± 5
(iii) the distance travelled by destroyer B. (2 Marks)
8.5 x 50 = 425±5
(iv) the bearing of N from L. (2 Marks)
200°
20. A number of people agreed to contribute equally to buy books worth KSh. 1200 for a school library.
Five people pulled out and so the others agreed to contribute an extra Shs. 10 each.
Their contributions enabled them to buy books worth Shs. 200 more than they originally expected.
(a) If the original numbers of people was x, write an expression of how much each was originally to contribute. (1 Mark)
1200/x
(b) Write down two expressions of how much each contributed after the five people pulled out. (2 Marks)
120/x + 10
1400/x-5
(c) Calculate the number of people who made the contribution. (5 Marks)
1400x-5 = 1200x = 10
1400x-1200(x-5)x(x-5)= 10
1400x-1200(x-5)x(x-5) = 10
200x + 6000 = 10×2 – 50x
20x + 600 = x2 – 5x
x2 + 15x – 40x – 600 = 0
x(x + 15) – 40(x + 15) = 0
(x-40)(x+15) = 0
x = 40 people
40 – 5 = 35
(d) Calculate how much each contributed. (2 Marks)
= 1400/35
= KSh. 40
21. Using a ruler and a pair of compasses only, draw a parallelogram ABCD, such that angle DAB = 750. Length AB = 6.0cm and BC = 4.0cm.
From point D, drop a perpendicular to meet line AB at N. (7 Marks)
(i) Measure length 0N (1 Mark)
Length of ON = 3.9cm±0.1
(ii) Find the area of the parallelogram. (2 Marks)
Area = 6 x 3.9
= 23.4cm2
22. The following measurements were recorded in a field book of a farm in metres (xy = 400m)
| Y | ||
|---|---|---|
| 400 | ||
| C60 | 350 | |
| 300 | 120D | |
| 240 | 100E | |
| 220 | 160F | |
| B100 | 140 | |
| A120 | 80 | |
| X |
(a) Using a scale of 1cm representing 4000cm, draw an accurate map of the farm. (3 Marks)
A = 12 x 60 x 60 = 1800m²
B = (60+100)2x 200 = 16000m²
C = (100+120)2 x 60 = 6600m2²
D = 12 x 120 x 80 = 4800m²
E = 12 x 160 x 220 = 17600m²
F = (160+100)2 x 20 = 2600m²
G = (100+120)2 x 60 = 6600m²
H = 12 x 120 x 100 = 6000m²
(b) If the farm is on sale at Kshs. 80,000.00 per hectare, find how much it costs. (7 Marks)
Total area = 62000m² = 62000/10000 = 6.2ha
1ha = 80,000
6.2ha = 8000 x 6.2/1
= KSh. 496,000.00
23. The table shows marks obtained by 100 candidates at Goseta Secondary School in Biology examination.
| Marks | 15-24 | 25-34 | 35-44 | 45-54 | 55-64 | 65-74 | 75-84 | 85-94 |
|---|---|---|---|---|---|---|---|---|
| Frequency | 6 | 14 | 24 | 14 | x | 10 | 6 | 4 |
(a)Determine the value of x (2 Marks)
6 + 14 + 24 + x + 10 + 6 + 4 = 100
x = 100 – 78
= 22
(b) State the modal class (1 Mark)
Modal class = 35 – 44
(c) Calculate the median mark (2 Marks)
median = 44.4 + 6/14 x 10
= 48.79
(d)Calculate the mean mark (5 Marks)
| Midpoint | f | xf |
|---|---|---|
| 19.5 | 6 | 117 |
| 29.5 | 14 | 413 |
| 39.5 | 24 | 948 |
| 49.5 | 14 | 693 |
| 59.5 | 22 | 1309 |
| 69.5 | 10 | 695 |
| 79.5 | 6 | 477 |
| 89.5 | 4 | 358 |
Σf = 100 Σxf = 50/10
Mean = xf/f
= 5010/100
= 50.10
24. In the diagram below, two circles, centres A and C and radii 7cm and 24cm respectively intersect at B and D. AC = 25cm.

(a) Show that angle ABC = 900. (3 Marks)
Triangle ABC
b²+h²=hy²
AB² + BC²= AC²
7² + 24² = 25²
49 + 576 = 625
625 = 625
(b) Calculate
(i) the size of obtuse angle BAD (3 Marks)
BAD = 2BAC
Sin θ =
24/25 θ = 73.74°
BAD = 73.74 x 2 = 147.48°
(ii) the area of the shaded part (4 Marks)
Area of kite = 1/2 x 7 x 24 x 2
Area of sector ABD = 147/360 x 3.14 x 72
= 62.87cm²
Area shaded = 168 – 62.87
= 105.13cm²

