2017 KCSE Mathematics Alt A Paper 2 Past Paper
Section I (50 marks)
1. The roots of a quadratic equation are x = -3/5 and x = 1. Form the quadratic equation in the form ax2 + bx + c = 0 where a, b and c are integers. (2 marks)
2. A tailor intended to subdivide a piece of cloth into 7 equal parts. She approximated 7 m to 0.14 m. Calculate the percentage error in the approximation. (3 marks)
3. A miller was contracted to make porridge flour to support a feeding program. He mixed millet, sorghum, maize and Omena in the ration 1:2:5:1. The cost per kilogram of millet was Ksh 90, sorghum Ksh 120, maize Ksh 30 and omena Ksh 150.
Calculate:
(a) the cost of one kilogram of the mixture;
(b) the selling price of 1 kg of the mixture if the miller made a 30% profit. (2 marks)
4. Without using mathematical tables or a calculator, evaluate 5/6log10 64 + log10 50 — 41og10 2. (3 marks)
5. In the figure below, PQRS is a cyclic quadrilateral. PQ = QR, PQR =105° and PS is parallel to QR.
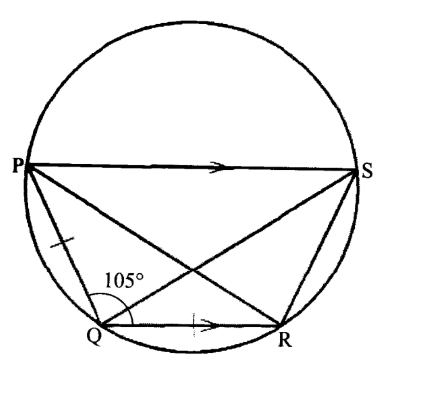
Determine the size of.
(a) ∠ PSR (1 mark)
(b)∠ PQS.(2 mark)
6. Make T the subject of s =
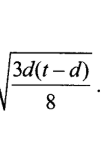
7. Simplify
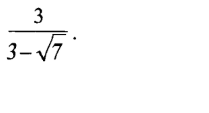
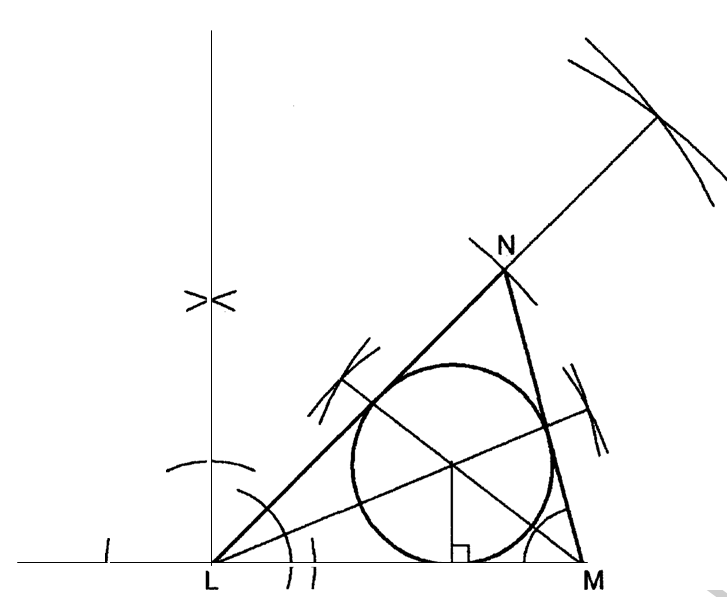
8. Using a ruler and a pair of compasses only, construct:
(a) a triangle LMN in which LM = 5 cm, LN = 5.6 cm and MLN = 450 .(2 marks)
(b) the circle that touches all the sides of the triangle. (3 marks)
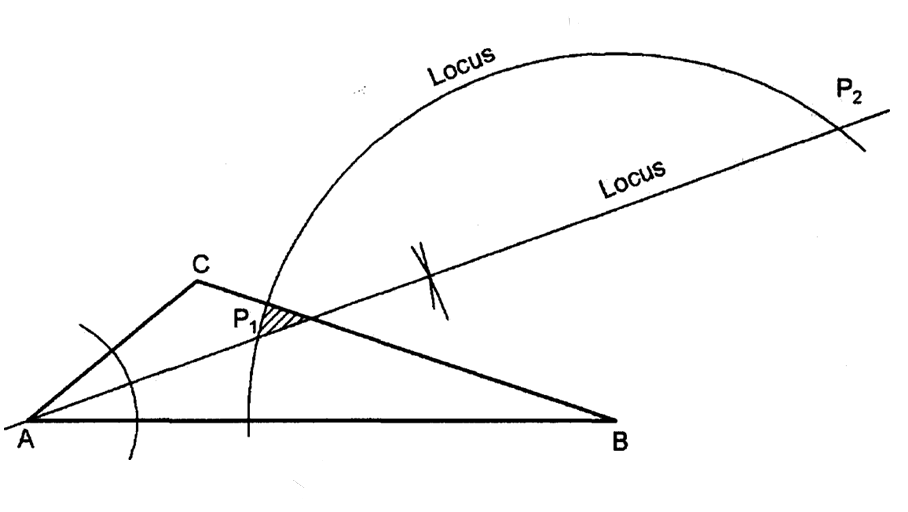
9. The figure below is a triangle ABC.
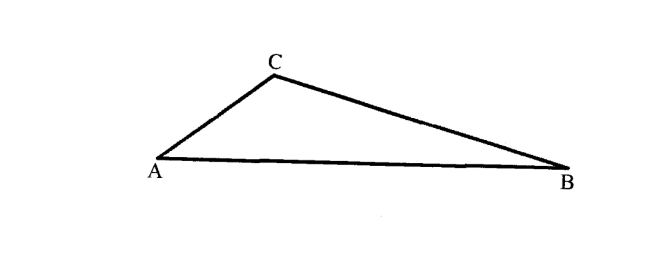
(a) On the triangle, locate the locus of points equidistant from AC and AB and 5 cm from B. (2 marks)
(b) Shade the region R, inside the triangle, which is less than 5 cm from B and nearer to AC than AB. (1 mark)
10. An aircraft took off from a point P (65° S, 76° W) and flew due North to a point Q. The distance between P and Q is 5400 rim.
Determine the position of Q. (3 marks)
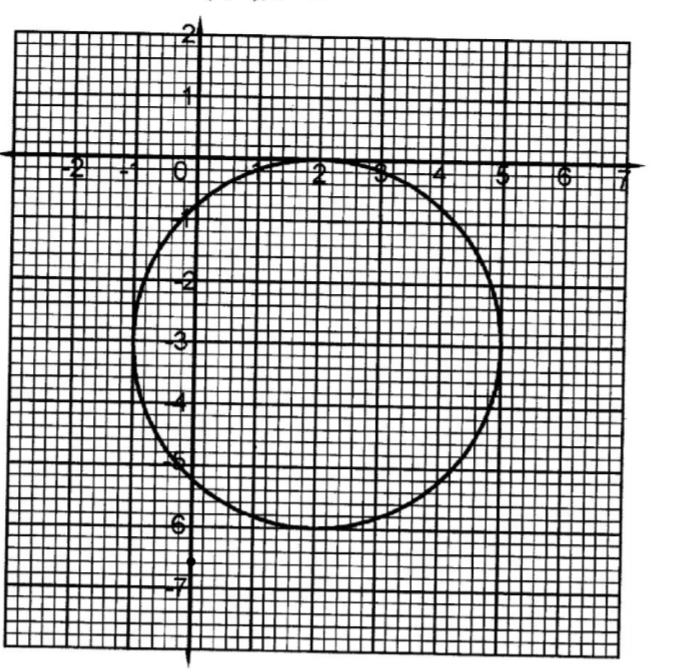
11. The equation of a circle is x2+ y2 – 4x + 6y + 4 = 0. On the grid provided, draw the circle.

(4 marks)
12. Determine the amplitude, period and the phase angle of the curve: 5/2 sin (40 + 60°)(3 marks)
13. A basket ball team scored the points in 6 matches: 10, 12, 14, 16, 28 and 30. Using an assumed mean of l5. Determine the standard deviation correct to 2 decimal places. (4 marks)
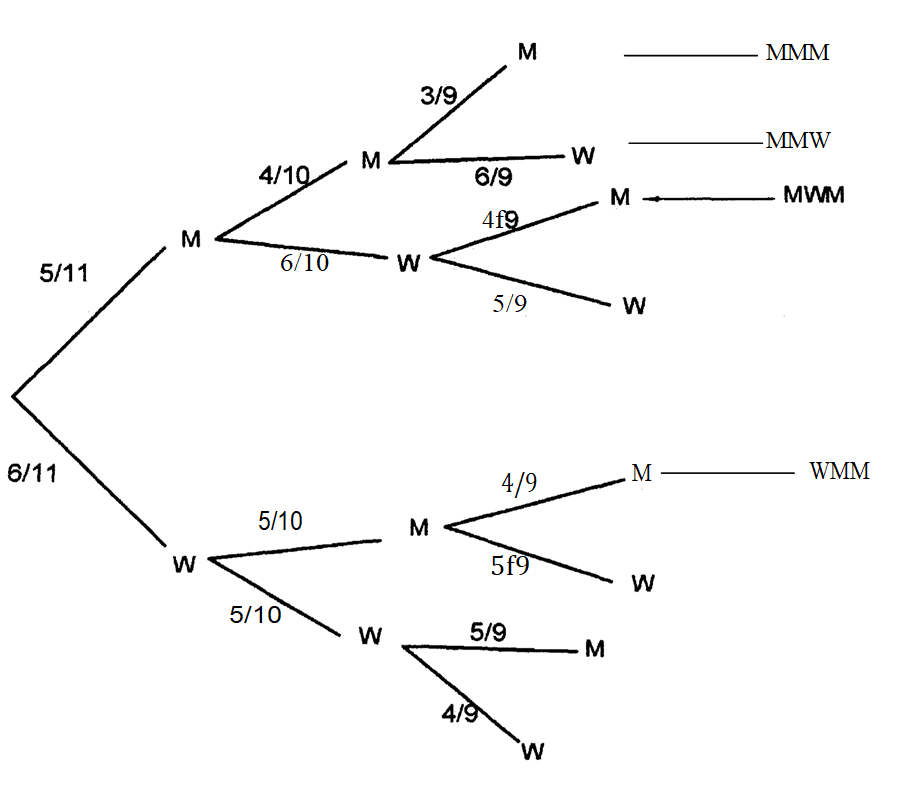
14. A committee of 3 people was chosen at random from a group of 5 men and 6 women. Find the probability that the committee consisted of more men than women. (4 marks)
15. The area of a triangle is 24 square units. The triangle is mapped onto image P by the matrix
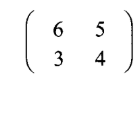
. Find the area of the image P.
16. Given that OA = 3i+ 4j+ 7k, OB= 4i + 3j + 9k and OC = i + 6j + 3k. show that points A, B and C are collinear. (2 marks)
Section B (50 marks)
17. Answer any five questions from this section in the spaces provided.
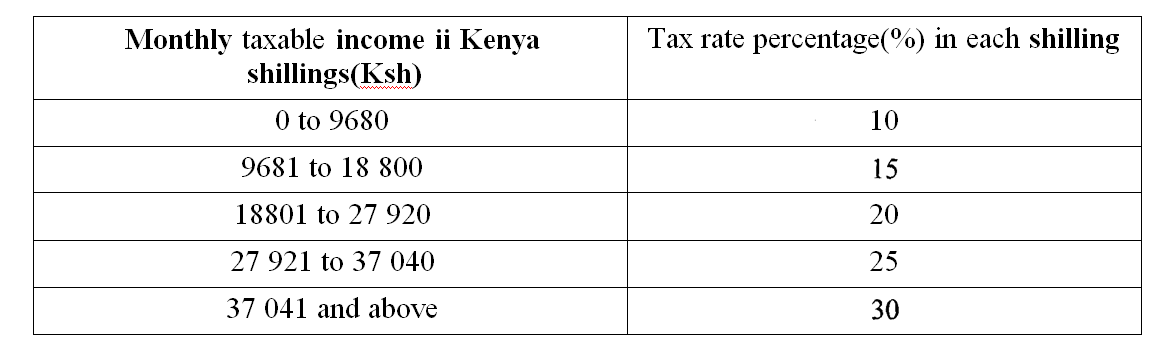
The income tax rates of a certain year u‘ere as shown in the table below:
In that year, Shaka’s monthly earnings were as follows: Basic salary Ksh 28600
House allowance Ksh 15 000
Medical allowanceKsh 3 200
Transport allowance Ksh 540
Shaka was entitled to a monthly tax relief of Ksh 1056.
(a) Calculate the tax charged on Shaka’s monthly earnings. (6 marks)
(b) Apart from income tax, the following monthly deductions were made; a Health Insurance fund of Ksh 500, Education Insurance of Ksh 1 200 and 2% of his basic salary for widow and children pension scheme. Calculate Shaka’s monthly net income from his employment. (4 marks)
18. The vertices ofa rectangle ABCD are: A(0,2), B(0,4), C(4,4) and D(4,2). The vertices of its image under a transformation T are; A’(0,2) , B’(0,4) , C’(8,4) and D’(8,2).
On the grid provided, draw the rectangle ABCD and its image A’B’C’D’ under T. (2 marks)

(ii) Describe fully the T. (3 marks)
(iii) Determine the matrix of transformation. (2 marks)
(b). On the same grid as in (a), draw the image of rectangle ABCD under a shear with line x — —2 invariant and A(0, 2) is mapped onto A”(0,0). (3 marks)
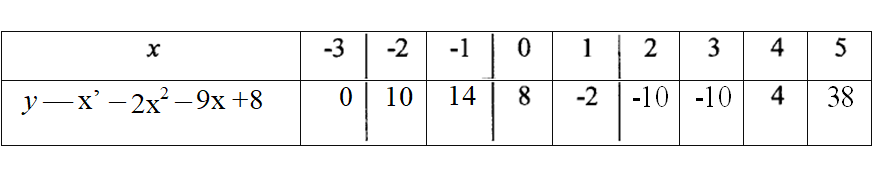
19. The table below shows values of x and some values off for the curve y = x3 — 2x2 — 9x + 8 for —3 ⋜ x ⋜ 5. Complete the table.

(b) On the grid provided, draw the graph of y = x3 — 2x2 — 9x + 8 for —3 ⋜ x ⋜ 5 for Use the scale; 1 cm represents 1 unit on the z-axis 2 cm represents 10 units on they-axis (3 marks)

(c) (i) Use the graph to solve the equation x2 — 2x3 — 9x + 8 = 0. (l mark)
(ii) By drawing a suitable straight line on the graph, solve the equation x2 – 2x2 — 11x + 6 = 0. (4 marks)
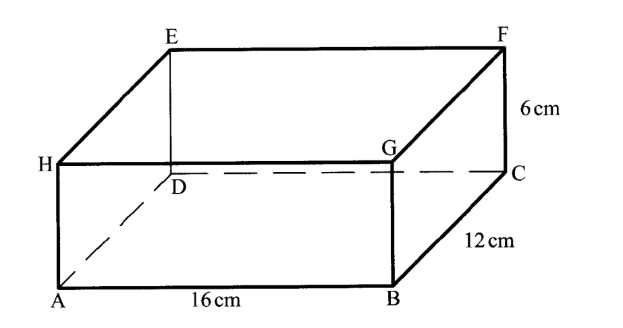
20. The figure below represents a cuboid ABCDEFGH in which AB — 16 cm, BC = 12 cm and CF = 6 cm.
(a) Name the projection of the line BE on the plane ABCD.
Calculate correct to 1 decimal place:
(i) the size of the angle between AD and BF; (2 marks)
(ii) the angle between line BE and the plane ABCD; (3 marks)
(iii) the angle between planes HBCE and BCFG. (2 marks)
(c) Point N is the midpoint of EF. Calculate the length BN, correct to 1 decimal place. (2 marks)
21. Three quantities X, Y and Z are such that X varies directly as the square root ofY and inversely as the fourth root of Z. When X = 64, Y = 16 and Z = 625.
(a) Determine the equation connecting X, Y and Z.
(b) Find the value of Z when Y = 36 and X = 160. (c) Find the percentage change in X when Y is increased by 44%. (4 marks)
22. A trader stocks two brands of rice A and B. The rice is packed in packets of the same size. The trader intends to order fresh supplies but his store can accommodate a maximum of 500 packets. He orders at least twice as many packets of A as of B.
He requires at least 50 packets of B and more than 250 packets of A. If he orders x packets of A and y packets of B,
(a) Write the inequalities in terms of x and y which satisfy the above information. (4 marks)
(b) On the grid provided represent the inequalities in part (a) above (4 marks)

(c) The trader makes a profit of Ksh 12 on a packet of type A rice and Ksh 8 on a packet of type B rice. Determine the maximum profit the trader can make. (2 marks)
23. (a) The 5° term of an AP is 82 and the 12° term is 103.
Find:
(i) the first term and the common difference; (3 marks)
(ii) the sum of the first 21 terms. (2 marks)
(b) A staircase was built such that each subsequent stair has a uniform difference in height. The height of the 6 stair from the horizontal floor was 85 em and the height of the 10° stair was 145 cm.
Calculate the height of the 1’t stair and the uniform difference in height of the stairs. (3 marks)
24. The length of a room is 3 m shorter than three times its width. The height of the room is a quarter of its length. The area of the floor is 60 m2.
(a) Calculate the dimensions of the room. (5 marks)
(b) The floor of the room was tiled leaving a border of width y m, all round. If the area of the border was 1.69m’, find:
(i) the width of the border;
(ii) the dimensions of the floor area covered by tiles.
2017 KCSE Mathematics Alt A Paper 2 Past Paper-Marking Scheme/Answers
Section A
1. The roots of a quadratic equation are x = -3/5 and x = 1. Form the quadratic equation in the form ax2 + bx + c = 0 where a, b and c are integers. (2 marks)
(X – 1) (5X – 3) = 0
5X25X + 3x – 3 = 0
5X2– 2x -3 = 0
2. A tailor intended to subdivide a piece of cloth into 7 equal parts. She approximated 7 m to 0.14 m. Calculate the percentage error in the approximation. (3 marks)
|Error| = 1/7 – 14/100
%Error 1/350 ÷ 1/7 x 100 1/350 x 7/1 x100
= 2%
3. A miller was contracted to make porridge flour to support a feeding program. He mixed millet, sorghum, maize and Omena in the ration 1:2:5:1. The cost per kilogram of millet was Ksh 90, sorghum Ksh 120, maize Ksh 30 and omena Ksh 150.
Calculate:
(a) the cost of one kilogram of the mixture;
M:S:M:O = 2:5:1 Cost of lkg of mixture
90 + 2(120) + 5(30) +150÷ 9
630/9
= Ksh 70
(b) the selling price of 1 kg of the mixture if the miller made a 30% profit.(2 marks)
130/100 x 70
= Ksh 91
4. Without using mathematical tables or a calculator, evaluate 5/6log10 64 + log10 50 — 41og10 2. (3 marks)
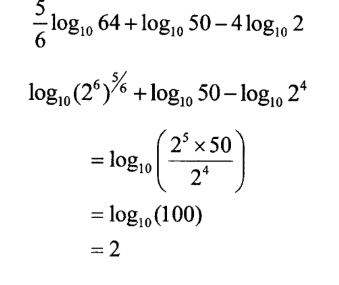
5. In the figure below, PQRS is a cyclic quadrilateral. PQ = QR, PQR =105° and PS is parallel to QR.

Determine the size of.
(a) ∠ PSR (1 mark)
180 -105 = 75°
(b)∠ PQS.(2 mark)
∠ PQS = ∠ SRP
∠ SRP = 180 —(37.5 + 75)
= 67.5°
6. Make T the subject of s =
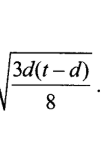
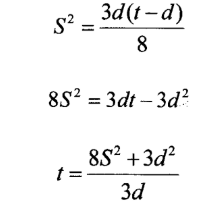
7. Simplify
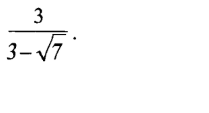
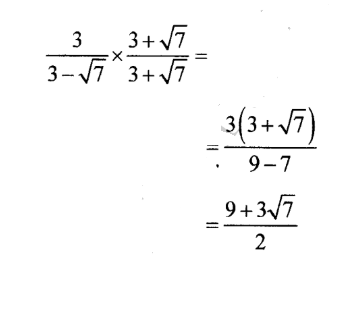
8. Using a ruler and a pair of compasses only, construct:
(a) a triangle LMN in which LM = 5 cm, LN = 5.6 cm and MLN = 450 .(2 marks)
(b) the circle that touches all the sides of the triangle. (3 marks)
9. The figure below is a triangle ABC.
(a) On the triangle, locate the locus of points equidistant from AC and AB and 5 cm from B. (2 marks)
(b) Shade the region R, inside the triangle, which is less than 5 cm from B and nearer to AC than AB. (1 mark)
10. An aircraft took off from a point P (65° S, 76° W) and flew due North to a point Q. The distance between P and Q is 5400 rim.
Determine the position of Q. (3 marks)
d —— 60 x 8
5400 = 60 x 8
5400/60 = 0
8 = 90ᵉ
Position of Q is (25°N, 76O W)
(65 – z)60 — 5400
x=25
Q(25°N, 70 w)
11. The equation of a circle is x2+ y2 – 4x + 6y + 4 = 0. On the grid provided, draw the circle.
x2 —4z +(—2)2 + y2 + 6y +(3)2 = —4 +(—2)2 +(3)2 (x — 2)2+(y+ 3)2 = 32 Centre (2,-3), r = 3
12. Determine the amplitude, period and the phase angle of the curve: 5/2 sin (40 + 60°)(3 marks)
sin(48 -I- 600 )
Amplitude = 2
Period = 90°
Phase angle = 60°
13. A basket ball team scored the points in 6 matches: 10, 12, 14, 16, 28 and 30. Using an assumed mean of l5. Determine the standard deviation correct to 2 decimal places. (4 marks)

14. A committee of 3 people was chosen at random from a group of 5 men and 6 women. Find the probability that the committee consisted of more men than women. (4 marks)
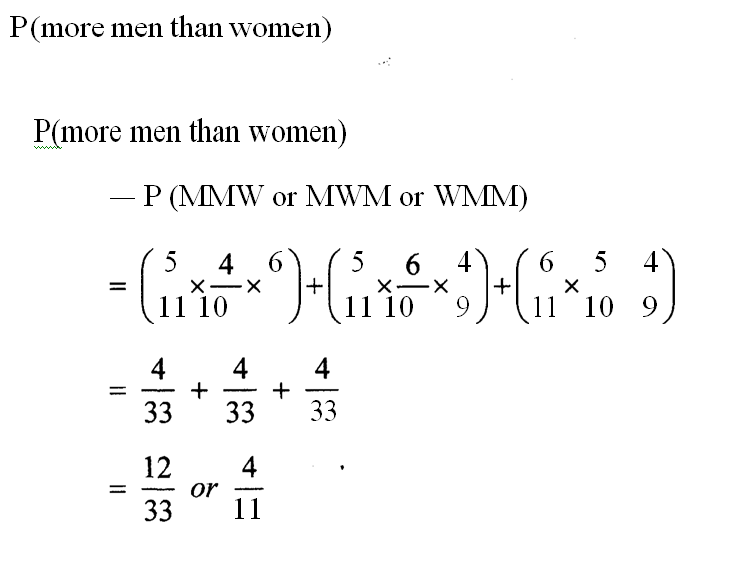
15. The area of a triangle is 24 square units. The triangle is mapped onto image P by the matrix
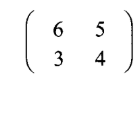
. Find the area of the image P.
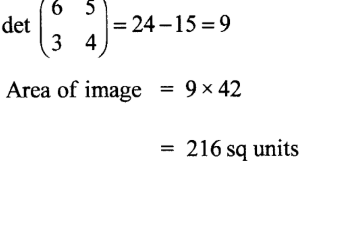
16. Given that OA = 3i+ 4j+ 7k, OB= 4i + 3j + 9k and OC = i + 6j + 3k. show that points A, B and C are collinear.(2 marks)
Section B (50 marks)
17. Answer any five questions from this section in the spaces provided.
The income tax rates of a certain year u‘ere as shown in the table below:

In that year, Shaka’s monthly earnings were as follows: Basic salary Ksh 28600
House allowance Ksh 15 000
Medical allowanceKsh 3 200
Transport allowance Ksh 540
Shaka was entitled to a monthly tax relief of Ksh 1056.
(a) Calculate the tax charged on Shaka’s monthly earnings. (6 marks)
Total earning/Taxable income
= Ksh (28600 + 15000 +3200 +540)
= Ksh 47340
Tax charged:
Up to 9680 —› 9680 ^ 10% = Ksh 968
9681 — 18800 9120 150/o = Ksh 1 368
18801 — 27920 —+ 9120 • 20% = Ksh 1 824
27924 — 37040 —+ 9120 25% — Ksh 2 280
Above 37040 10300 30% = Ksh 3 090
Total tax less relief:
(968 +1 368+1 824 +2 280+3 090) — 1 056 = Ksh 8 474
(b) Apart from income tax, the following monthly deductions were made; a Health Insurance fund of Ksh 500, Education Insurance of Ksh 1 200 and 2% of his basic salary for widow and children pension scheme. Calculate Shaka’s monthly net income from his employment. (4 marks)
Monthly deductions:
2% of Ksh 28 600 = Ksh 572
Total deductions
Ksh (8 474 500 + 1 200 + 572) = Ksh 10 746
Net income = Ksh (47 340 — 10 746) Ksh 36 594
18. The vertices ofa rectangle ABCD are: A(0,2), B(0,4), C(4,4) and D(4,2). The vertices of its image under a transformation T are; A’(0,2) , B’(0,4) , C’(8,4) and D’(8,2).
On the grid provided, draw the rectangle ABCD and its image A’B’C’D’ under T. (2 marks)
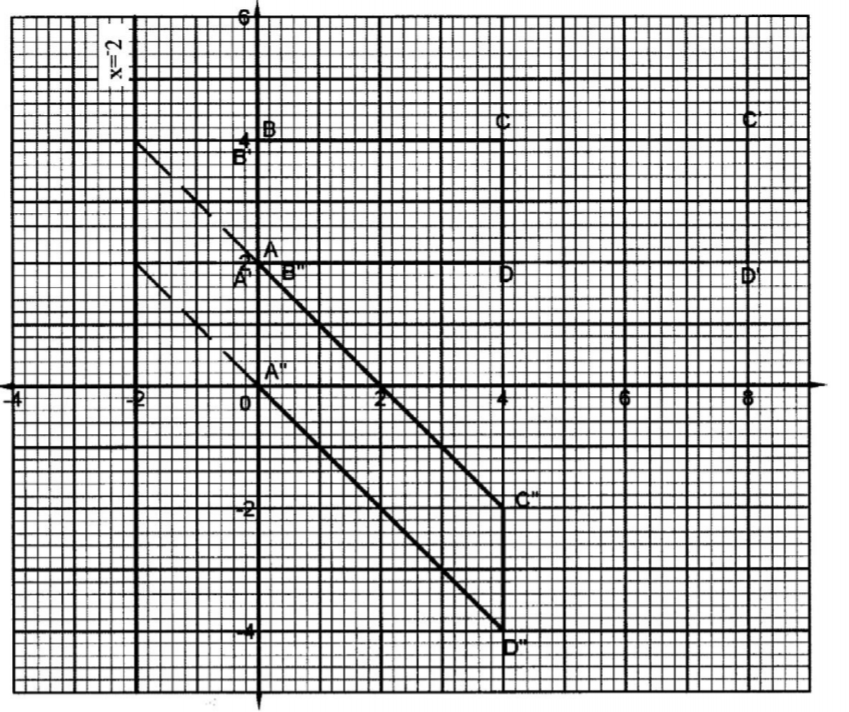
(ii) Describe fully the T. (3 marks)
T is a stretch
S.F. = 2
x = 0 or y- axis invariant
(iii) Determine the matrix of transformation. (2 marks)
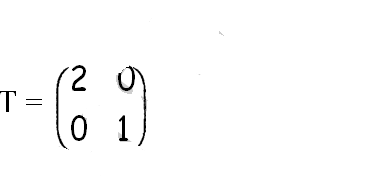
(b). On the same grid as in (a), draw the image of rectangle ABCD under a shear with line x — —2 invariant and A(0, 2) is mapped onto A”(0,0). (3 marks)
Invariant line identified and used
A’,B’,C’and D’plotted A”B”C”D” drawn correctly
19. The table below shows values of x and some values off for the curve y = x3 — 2x2 — 9x + 8 for —3 ⋜ x ⋜ 5. Complete the table.
(b) On the grid provided, draw the graph of y = x3 — 2x2 — 9x + 8 for —3 ⋜ x ⋜ 5 for Use the scale; 1 cm represents 1 unit on the z-axis 2 cm represents 10 units on they-axis (3 marks)
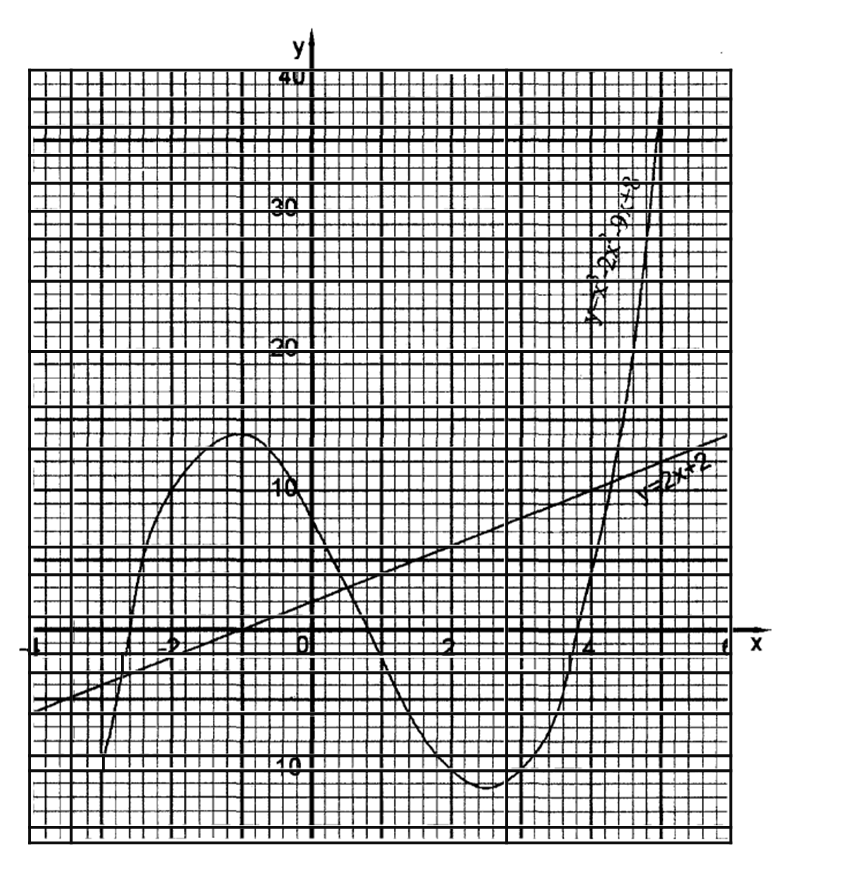
(c) (i) Use the graph to solve the equation x2 — 2x3 — 9x + 8 = 0. (l mark)
Roots x = -2.6, 0.8, 3.8 Or for (0, 0), x = — 2.6, 0, 3.8
(ii) By drawing a suitable straight line on the graph, solve the equation x2 – 2x2 — 11x + 6 = 0. (4 marks)
y = x3 – 2x3 — 9x + 8
o = x3 — 2x2 — 11x + 6
2x + 2
y =2x + 2 drawn
Roots are -2.7, 0.5, 4.3
For (0, 0) ; x = -2.7, — 0.1 and 4.3
20. The figure below represents a cuboid ABCDEFGH in which AB — 16 cm, BC = 12 cm and CF = 6 cm.

(a) Name the projection of the line BE on the plane ABCD.
Projection of BE is BD
Calculate correct to 1 decimal place:
(i) the size of the angle between AD and BF; (2 marks)
Angle between line AD and BF
=tan–(16/6)
12
= 26.6°
(ii) the angle between line BE and the plane ABCD; (3 marks)
Angle between line BE and plane ABCD
BD = √ 122 + 162
= 20
Tan (DBE) = 6/20
ZDBE = tank s 6/20
16.70
(iii) the angle between planes HBCE and BCFG. (2 marks)
Angle between HBCE and BCFG. tan° 16
Tan -1 16/6
69.40
(c) Point N is the midpoint of EF. Calculate the length BN, correct to 1 decimal place. (2 marks)
BF = √ 12 + 62
= √ 180
BN = √ 180 + 82
=15.6cm
21. Three quantities X, Y and Z are such that X varies directly as the square root ofY and inversely as the fourth root of Z. When X = 64, Y = 16 and Z = 625.
(a) Determine the equation connecting X, Y and Z.
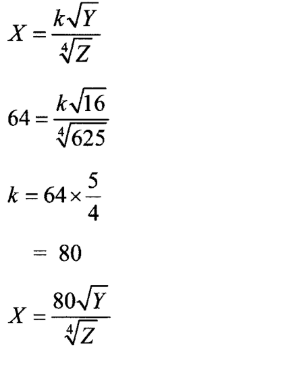
(b) Find the value of Z when Y = 36 and X = 160.
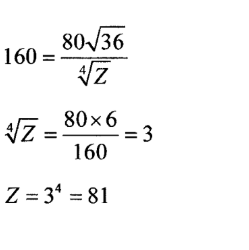
(c) Find the percentage change in X when Y is increased by 44%. (4 marks)

22. A trader stocks two brands of rice A and B. The rice is packed in packets of the same size. The trader intends to order fresh supplies but his store can accommodate a maximum of 500 packets. He orders at least twice as many packets of A as of B.
He requires at least 50 packets of B and more than 250 packets of A. If he orders x packets of A and y packets of B,
(a) Write the inequalities in terms of x and y which satisfy the above information. (4 marks)
x+y⋜ 500
x⋝ 2y
y = ⋝
x = > 250
(b) On the grid provided represent the inequalities in part (a) above (4 marks)
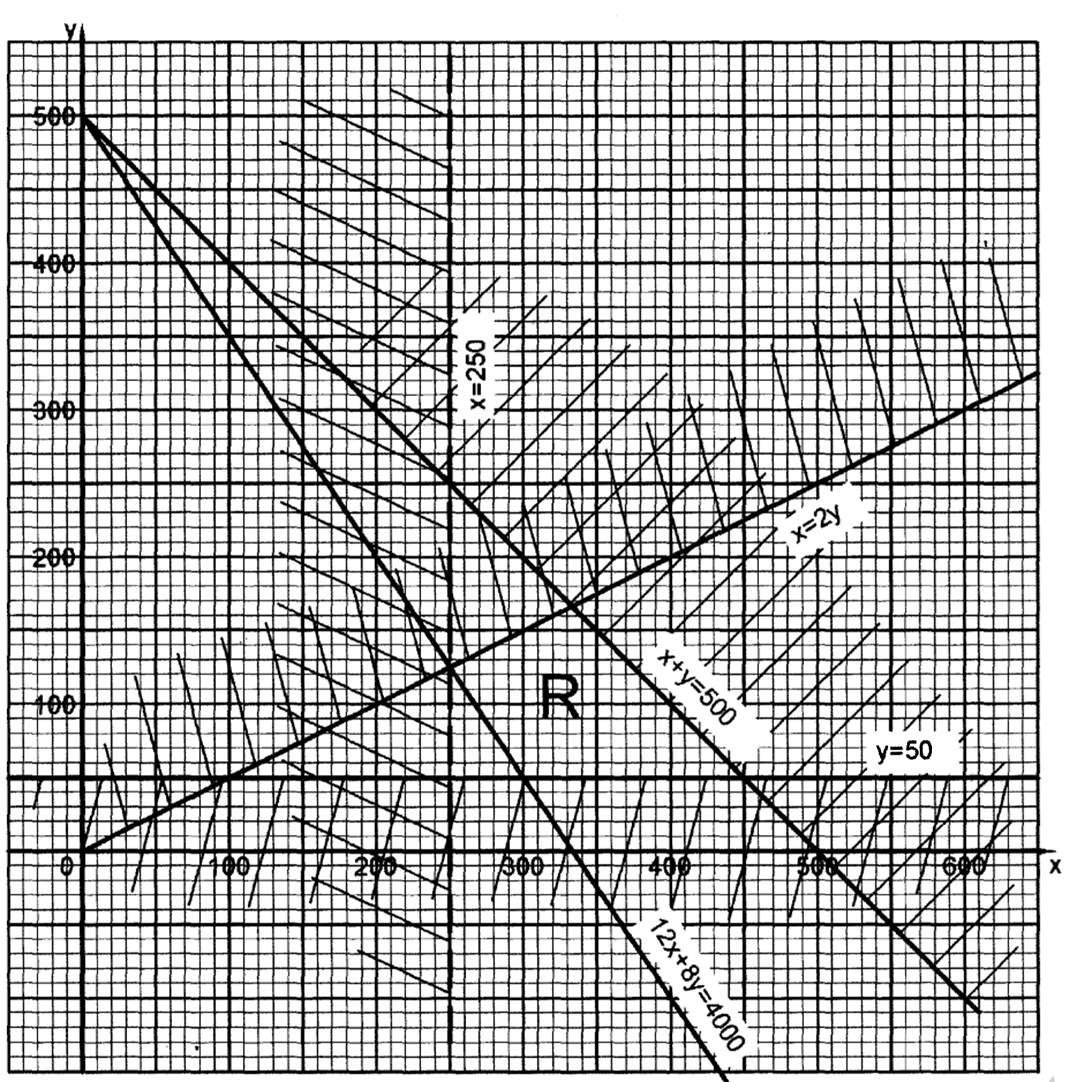
x+y ⋜ 500 B1
x > 250 2y B1
y ⋜ 50 B1
x > 250 250
(c) The trader makes a profit of Ksh 12 on a packet of type A rice and Ksh 8 on a packet of type B rice. Determine the maximum profit the trader can make. (2 marks)
Search line 12x + 8y = 4000
For maximum profit x = 450, y = 50
Maximum profit = 12 x 450+50 x 8 Ksh 5800
23. (a) The 5° term of an AP is 82 and the 12° term is 103.
Find:
(i) the first term and the common difference;(3 marks)
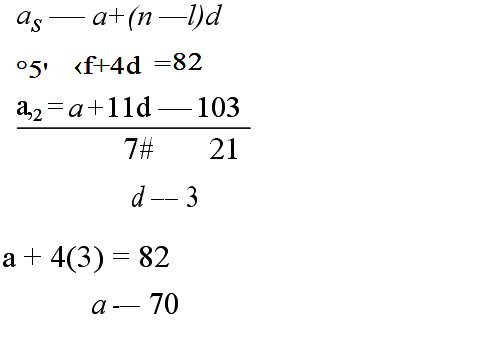
(ii) the sum of the first 21 terms. (2 marks)
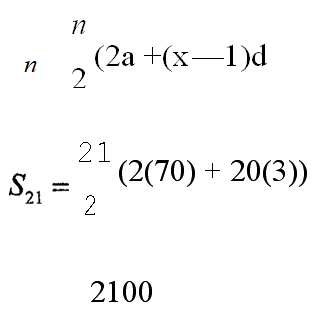
(b) A staircase was built such that each subsequent stair has a uniform difference in height. The height of the 6 stair from the horizontal floor was 85 em and the height of the 10° stair was 145 cm.
Calculate the height of the 1’t stair and the uniform difference in height of the stairs. (3 marks)
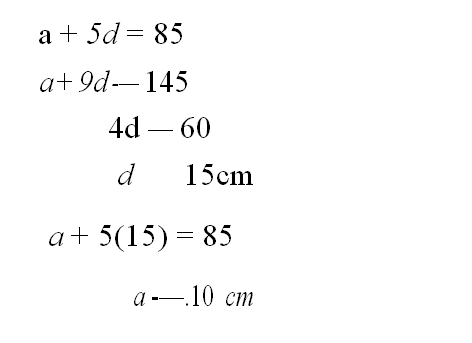
24. The length of a room is 3 m shorter than three times its width. The height of the room is a quarter of its length. The area of the floor is 60 m2.
(a) Calculate the dimensions of the room. (5 marks)
Let x be the width (3 —3) = 60
3 — 3z — 60 = 0
x2 — x — 20 = 0
(x — 5)(x + 4) — 0
x —— 5 or x —— —4
.’. width x —— 5m
Length = 12m Height = 3m
(b) The floor of the room was tiled leaving a border of width y m, all round. If the area of the border was 1.69m’, find:
(i) the width of the border;
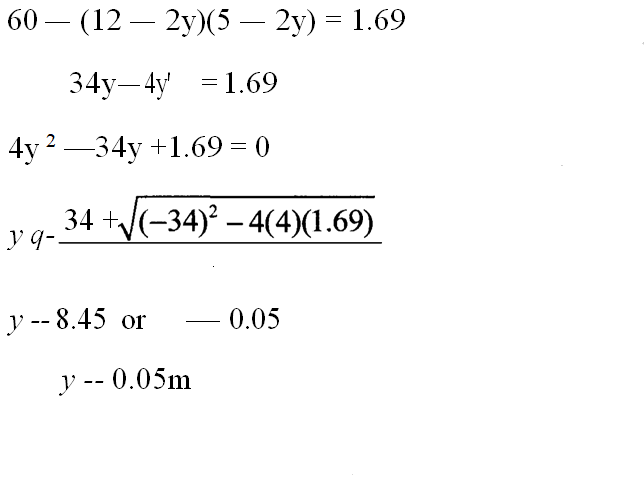
(ii) the dimensions of the floor area covered by tiles.
Dimensions or tiled area Length = 12 — 0.1 = 11.9 m
Width = 5 — 0.1 = 4.9 m

